Тензор
Те́нзор (лат. tensus, «хивре», «кару») — математикăра тата физикăра усă куракан линилле тата нумай компонентлă алгебрăлла объектăн хай векторла уçлăхăн вĕçсĕр мар виçеллĕ (хапаллă) талккăшĕнче палăртнă тĕсĕ (линилле алгебрăн объекчĕ). Физикăра пек чылай чухне 3 виçеллĕ уçлăх е 4 виçеллĕ уçлăх-вăхăт пулать, леш тензорăн компоненчĕсем пек хире-хирĕç çыхăннă физикăлла капсен координачĕсем (проекцийĕсем) пулаççĕ.
Кăшт ансатрах (çирĕпех мар) чĕлхепе кăна çапла палăртма пулать[1].
- тензор вăл уçлăхри геометрилле е физикăлла пĕр-пĕр объекта тензор компоненчĕсем текен капсен таблици пек кăтартни;
- асăннă компонентсем йышăннă пуçлав тытăмĕнчен килеççĕ тата тепĕр координатсем патне куçнă чухне улшăвланаççĕ (трансформациленеççĕ);
- компонентсем улшăвланаççĕ, анчах та инвариант текен хăшпĕр капсем çаплах юлаççĕ.
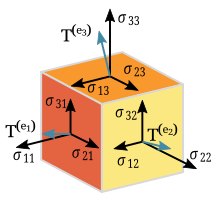
Тензор вăл — скаляр, вектор, ковектор, линилле оператор тата билинилле форма тенисене анлăлатса тата пĕрлештерсе тăракан математикăлла объект. Тензорсене тишкерекен дисциплинăна тензорла шутлав теççĕ.
Мĕнле те пулин базисра (пуçлав тытăмĕнче) тензора нумай виçеллĕ тата хисепсемпе (тензор компоненчĕсемпе) тултарнă d х d x ... x d таблица пек кăтартассĕ (хутланакансен шутне кунта тензорăн валентлăхĕ теççĕ). Базис улшăнсан компонентсем улшăнаççĕ, тензорĕ хăй çаплах юлать.
Тензорсемпе физикăра усă курни физикăлла саккунсемпе танлăхсене тарăнрах ăнланма пулăшать тата, пĕр-пĕринпе хире-хирĕçле çыхăннă физикăлла капсене пĕр тензор пек кăтартнă май, çырав ансатланать тата ăна, çырава, пуçлав тытăмĕнчен килмен пĕтĕмĕшле ковариантла формăпа кăтартма май пур.
Паллă тăвасси
тӳрлетВекторла V уçлăх çийĕнчи (m, n) ранглă тензор вăл m чухлĕ V уçлăхсене n чухлĕ V* çумкÿлĕмле уçлăхсем çине тензорла хутланин элеменчĕ (е линилле функционалсен уçлăхĕсене (1-формăсене) V çине хутланин)
Хисепсен m+n сумми тензор валентлăхĕ пулса тăрать. Çавăн пекех, (m, n) ранглă тензора m хут контравариантлă тата n хут ковариантлă теççĕ.
Тензорла объектсене паллă тăвасси
тӳрлетпек паллă тунă тензор мĕне кăтартнине чухлас тесен вăл пĕр пуçлав тытăмĕнчен тепĕр пуçлав тытăмне епле куçнине пăхас пулать:
кунта:
Вуламалли
тӳрлет- Акивис М. А., Гольдберг В. В. Тензорное исчисление. — М.: Наука, 1969;
- Димитриенко Ю. И. Тензорное исчисление: Учеб. пособие. — М.: Высшая школа, 2001. — 576 с. ISBN 5-06-004155-7.
- Коренев Г. В. Тензорное исчисление: Учеб. пособие. — М.: Издательство МФТИ, 2000. — 240 с. — ISBN 5-89155-047-4.
- Кочин Н. Е. Векторное исчисление и начала тензорного исчисления (9-е издание). — М.: Наука, 1965;
- Мак-Коннел А. Дж. Введение в тензорный анализ с приложениями к геометрии, механике и физике. — М.: Физматлит, 1963;
- Номидзу К. Группы Ли и дифференциальная геометрия. — М.: ИЛ, 1960;
- Победря Б. Е. Лекции по тензорному анализу: Учеб. пособие. (3-е изд.). — М.: Изд-во МГУ, 1986;
- Рашевский П. К. Риманова геометрия и тензорный анализ (3-е издание). — М.: Наука, 1967;
- Шарипов Р. А. Быстрое введение в тензорный анализ. — БашГУ.
Асăрхавсем
тӳрлет- ^ Гаврилов, Сергей. Тензорное исчисление для «чайников»
| Урăх чĕлхе уйрăмĕнче туллирех статья пур Tensor(акăлч.) Çак статьяна куçарса эсир проекта пулăшма пултаратăр.
|

