Стерадиан

Стерадиа́н (чăвашла кăтарту: ср, тĕнчери кăтарту: sr; ав.гр. στέρεος — хытă, клăпăшлă, уçлăхла, тата лат. radius — пайăрка) — ĕскерле кĕтесе виçмелли пĕрчĕ.

1 стерадиан чухлĕ ĕскерле кĕтесе ÿкерсе кăтартни

1 стерадиан чухлĕ ĕскерле кĕтес тăвакан çаврака конусăн $2\theta$ сарăлу кĕтесĕ

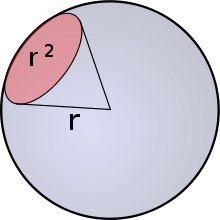
r радиуслă сферăн варринчи тăрăллă тата 1 стерадиан чухлĕ ĕсерле кĕтес çав сферăран r² чухлĕ лаптăк касса кăларать. Енчен те ку ĕскерле кĕтес çаврака конус пек пулсан, $\phi$ сарăлу кĕтесĕ çапла пулать:

$\phi =2\theta =2\arccos \left(1-{\frac {1}{2\pi }}\right)\approx 1.144\,{\text{rad}},$

(çывхартсан 65,541° е 65°32′28″).

Сферăн варинчен сăнанакан унăн çийĕ ${4\pi }$ стерадиан чухлĕ ĕскерле кĕтес тăвать; çавăн пекех, 1 ср = 1/4π ≈ 0,0796, тулли ĕскерле кĕтеср (сфера) тĕлĕшпе илес пулсан, е (180/π)² ≈ 3282,8 , иккĕмĕш капашлă градус тĕлĕшпе илсен. /

Çĕр варринчен тухакан пайăркасем Çĕр çинчи тĕрлĕ лаптăксем витĕр иртсен еплерех ĕскерле кĕтессем туни

Стерадиан Тĕнчери пĕрчĕсен тытăмне (СИ) кĕрет. 1995-мĕш çулхи йышăну тăрăх, стерадиан СИри хапасăр пĕрчĕ шутланать, çав вăхăтрах унăн ятарлă ячĕ тата символĕ пур, вĕсене усă курма та усă курмасăр тăма та май пур, пĕтĕмпех кăмăлтан тата кирлĕлĕхрен килет.

$\Omega$ ĕскерле кĕтесе тупмалли формула, енчен те çаврака конус тăрринчи $\phi$ кĕтес паллă пулсан, ак çапла:

$\Omega =2\pi [(1-\cos(\phi /2)].$

Истори

«Стерадиан» (акăл. steradian) термина чи малтан Дж. Холстедом^[en] хăйĕн «Метрикăлла геометри» кĕнекинче (акăл. Metrical geometry. An elementary treatise on mensuration, Boston: Ginn, Heath & co., 1881) кĕртнĕ.